Übungen zum historischen Lösen Quadratischer Gleichungen

Der Aufgabenpool „Übungen zum historischen Lösen Quadratischer Gleichungen“ umfasst ein Gruppenpuzzle zu historischen Lösungsverfahren quadratischer Gleichungen. Dabei wird jedes Übungsblatt von einer Expertengruppe bearbeitet und die entsprechende Aufgabe auf dem Ergebniszettel gelöst. Nach der Bearbeitung finden sich die Stammgruppenmitglieder zusammen. Jeder Experte erklärt sein Übungsblatt und es wird gemeinsam der Ergebniszettel bearbeitet. Das schülerzentrierte, selbstständige und entdeckende Lernen des Aufgabenpools wird durch Lernhilfen unterstützt.

Das Material kann fakultativ als Erarbeitung und Übung zum Lernbereich 1 „Funktionen und Potenzen“ des sächsischen Lehrplans für Gymnasien, Klasse 9, genutzt werden.

In dem Einführungsvideo bittet ein Pharao um Hilfe bei der Bearbeitung eines mathematischen Problems. Unter Verwendung historischer Lösungsverfahren wird dies im Laufe der Unterrichtseinheit gelöst. Der Ergebniszettel beginnt mit dem Problem des Pharaos, welches in Formelsprache wiedergegeben ist. Die einzelnen Verfahren werden auf dem Ergebniszettel aufgegriffen und am Ende wird das Problem des Pharaos gelöst.

Das Material enthält vier differenzierte Übungsblätter zu historischen Lösungsverfahren, die auch einzeln behandelt werden können.

Ein Übungsblatt behandelt das Heron-Verfahren. Die Schülerinnen und Schüler lernen das Heron-Verfahren anhand ausführlicher Erklärungen und einer Beispielaufgabe kennen. Sie üben das Verfahren mit Hilfe eines Lückentexts und führen das komplette Verfahren eigenständig durch.

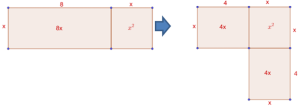
Ein weiteres Übungsblatt behandelt „Quadratische Gleichungen lösen wie al-Khwarizmi“. Es dient der geometrischen Visualisierung des Prinzips der quadratischen Ergänzung und bietet eine Alternative zum rechnerischen Lösen quadratischer Gleichungen mit Hilfe von geometrischen Zeichnungen.
Das dritte Übungsblatt bietet eine kurze, chronologische Reise durch die historische Entwicklung der Lösung quadratischer Gleichungen. Man reist von den alten Babyloniern über das Deutschland der Reformationszeit mit dem Verfahren von Michael Stifel bis zu unserer heutigen Zeit und der allgemein bekannten p-q-Formel.

Das vierte Übungsblatt bietet eine Einführung in den Wurzelsatz von Vieta. Dies wird ergänzt durch den Beweis, der über ein Beweispuzzle bearbeitet wird. Weiterhin werden vielfältige Anwendungen des Wurzelsatzes als Aufgaben gestellt.
Die Übungsblätter sind in ein Gruppenpuzzle eingebettet. Dabei bildet jedes Übungsblatt eine Station, die gemeinsam in Expertengruppen mit Hilfe des Laufzettels ausgewertet werden. Das schülerzentrierte, selbstständige und entdeckende Lernen des Aufgabenpools wird durch Lernhilfen unterstützt und ermöglicht es den Gruppen ihr Übungsblatt und den Laufzettel zu bearbeiten.

Intro:

Outro: