Der Aufgabenpool „Sätze am Kreis“ umfasst eine Präsentation zur Einführung in die Beweislogik, eine Sammlung differenzierter Übungsblätter zur Einführung der Sätze am Kreis, eine Lerntheke und eine Leistungskontrolle.
Das Material kann zur Einführung, Festigung und Sicherung relevanter Inhalte der Lernbereiches 1 „Geometrie in der Ebene“ des sächsischen Lehrplans für Gymnasien, Klasse 7, genutzt werden.
Die Power-Point-Präsentation „Einführung zur Beweislogik“ führt die Lernenden anhand von Alltagssituationen an Wenn-dann- und Genau-dann-wenn-Aussagen heran. Dabei wird insbesondere auf die Umkehrbarkeit dieser Aussagen eingegangen.
Das Material enthält eine Übersicht und fünf differenzierte Übungsblätter zur Einführung der Sätze am Kreis (Satz des Thales, Peripheriewinkelsatz, Peripherie-Zentriwinkelsatz, Sehnen-Tangentenwinkelsatz, Satz über gegenüberliegende Winkel im Sehnenviereck). Durch diese Übungsblätter führen fünf Kreismenschen, die dem jeweiligen Satz nachempfunden sind.
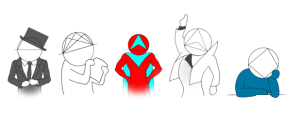 Diese Fünf moderieren die zugehörigen Arbeitsblätter, geben Hilfestellungen und stellen darüber hinaus ein einprägsames Bild der Sätze für die Schülerinnen und Schüler dar.
Diese Fünf moderieren die zugehörigen Arbeitsblätter, geben Hilfestellungen und stellen darüber hinaus ein einprägsames Bild der Sätze für die Schülerinnen und Schüler dar.
Alle Übungsblätter sind ähnlich aufgebaut. Sie bestehen aus drei Phasen, in denen die Lernenden zunächst angeleitet werden, eine Vermutung über den Inhalt der Sätze zu finden, diese anschließend an Beispielen zu überprüfen und sie abschließend zu beweisen. Das Übersichtsblatt dient zur Zusammenfassung der zentralen Aussagen der fünf Sätze. Das Material wurde so gestaltet, dass der Satz des Thales als erster dieser Sätze mit der gesamten Klasse erarbeitet wird. Die verbleibenden vier Sätze werden in Kleingruppen erarbeitet und präsentiert.
Die Lerntheke dient als Festigung und Übung für zentrale Inhalte des Lernbereiches über die Sätze am Kreis hinaus. Zu Beginn steht hier eine Checkliste, in der die Schülerinnen und Schüler selbst einschätzen, ob sie die einzelnen Inhalte sehr gut, grundlegend oder noch nicht ausreichend beherrschen.
 Basierend auf ihrer Selbsteinschätzung teilt die Checkliste für jedes Arbeitsblatt eine passende Schwierigkeitsstufe zu. Im Anschluss bearbeiten die Lernenden Aufgaben zu den Themen „Basiswissen“, „Konstruieren“, „Anwenden“ sowie „Sätze und Beweise“. Für jeden Bereich ist ein Arbeitsblatt vorhanden, welches die Schülerinnen und Schüler auf dem gewählten Niveau bearbeiten.
Basierend auf ihrer Selbsteinschätzung teilt die Checkliste für jedes Arbeitsblatt eine passende Schwierigkeitsstufe zu. Im Anschluss bearbeiten die Lernenden Aufgaben zu den Themen „Basiswissen“, „Konstruieren“, „Anwenden“ sowie „Sätze und Beweise“. Für jeden Bereich ist ein Arbeitsblatt vorhanden, welches die Schülerinnen und Schüler auf dem gewählten Niveau bearbeiten.
Die abschließende Leistungsüberprüfung schließt sich inhaltlich an die Lerntheke an und prüft entsprechende Inhalte in Form einer schriftlichen Leistungskontrolle ab.

Das könnte Sie auch interessieren
Auswerten von Daten
Modellierung mit trigonometrischen Funktionen
Wiederholung von Funktionen (Gymnasium)